Welcome to the Dopex Essentials series that helps everyone get acquainted with the basics of options trading. Everyone should start with the first part of the series to grasp the knowledge throughout.
As an options trader, you will face the following risks:
- Delta Risk (Directional risk): Change in the price of the underlying asset
- Gamma Risk: Changes in the Delta of a position
- Theta Risk (Theta/Time Decay): Time past
- Vega Risk (Volatility): Changes in expected volatility
So far in this series, we have discussed Greeks like Delta, Gamma, and Theta. In this article, we will discuss the Greek regarding expected volatility – Vega.
Here is the complete list of parts of this Series:
In addition to this series, people can also refer to the following articles to better understand Option Trading and Dopex!
There is a glossary of terms at the end of the article, so if you come across unfamiliar terms, scroll down for reference!
Jumi & Ultraman

We all know that as volatility increases, the prices of assets tend to start moving wildly and unpredictably.
There are two options sellers, Jumi and Ultraman. Jumi sells some $DPX puts and Ultraman sells some $DPX calls. In this example, $DPX is trading at $10,000 and let’s assume that an increase in volatility could cause DPX to start swinging anywhere between $9,000 and $11,000.
Scenario A
When $DPX hits $9,000, all the put sellers in the market (including Jumi) will start to worry because the put option now has a higher chance of ITM at expiration.
Scenario B
On the other hand, when $DPX hits $11,000, all the call option sellers in the market (including Ultraman) will start to panic because calls now have a higher chance of ITM at expiration.
Conclude
What we can deduce from the above example is that regardless of the option (long or short), as volatility increases, the option is more likely to ITM at expiration.
The Nifteas Dilemma
Let’s now look at how the scenarios we just discussed above would affect an options trader’s trading approach, using yet another example:
Let’s say a Nifteas trader wants to sell some $DPX call options at $10,000 with a 10-day expiry. No intrinsic value yet, but has time value. Let’s say the options premium is $420 – ask yourself, if you were in Nifteas’ position, would you sell the options?
Sure, Nifteas could write the options and pocket the $420 premium. DWhat if there’s a big Fed conference coming up, and that means 10-day volatility is likely to increase, do you think Nifteas will still go ahead and write options with price $420 USD?
It’s likely he won’t because as mentioned earlier, increased volatility increases the likelihood of ITM options expiring. So there are chances that Nifteas could lose the entire $420 premium. So if all option sellers fear volatility, what incentive do they have to sell options?
The answer is simple – a higher premium.
When volatility increases or is expected to increase, options sellers begin to fear that options may move into ITM status.
However, if the profits from premium are attractive enough, people will have reason to be less afraid. So the premium on call and put options will increase as expected volatility increases.
Vega is a Greek indicator that helps options traders estimate how much option prices will increase or decrease as expected volatility increases or decreases.
Vega
What is Vega?
Vega measures the risk from changes in the expected future volatility of the underlying asset price
Unlike Delta which measures actual price changes, Vega measures these change in expectations about future fluctuations. Greater volatility makes options more expensive because they are more likely to be exercised by the buyer at expiration.
Vega tells us how much an option price will increase or decrease as expected volatility increases or decreases. While the option seller benefits from a reduction in expected volatility, the option buyer bears the risk.
It is important to note that implied volatility reflects price action in the market. As option prices increase because there are more buyers, we can expect an increase in expected volatility.
Call option traders benefit from the market’s expectation of an increase in the underlying asset’s price, and put option traders benefit from the market’s expectation of a decrease in the underlying asset’s price. Therefore, call options have a positive Vega value and put options have a negative Vega value.
Important properties:
- Due to changes in expected volatility, the value of Vega may fluctuate even if the price of the underlying asset remains unchanged.
- The magnitude of Vega can increase with sudden changes in the price of the underlying asset.
- As the option gets closer to its expiration date, the magnitude of Vega decreases.
Example of Vega in options
Vega is calculated as the expected change in the price of an option for every 1% change in expected volatility. The following table shows how the price of an option is likely to change in response to changes in the expected volatility index:
|
Options Price |
Vega |
Option price with expected volatility +1% |
Option price with expected volatility -3% |
|---|---|---|---|
|
$100 |
0.3 |
$100.3 |
$99.1 |
|
$10 |
0.25 |
$10.25 |
$9.25 |
|
$1.15 |
0.01 |
$1.16 |
$1.12 |
What we can deduce from this (focusing on the $100 option) is that a Vega value of 0.30 represents a $0.30 increase in option price for every 1% increase in expected volatility, and vice versa. . With an expected 3% decrease in volatility, the value of the option is expected to be less than $0.90. Let’s try the calculation for $10 and $1.15 options.
To estimate the expected price of an option corresponding to a 1% increase in expected volatility, simply add the option’s Vega coefficient to its price. For a 1% expected decrease in volatility, the price of an option can be estimated by subtracting the value of Vega.
Vega vs Strike
Let’s analyze the following chart to see which options are most sensitive to the Vega index.
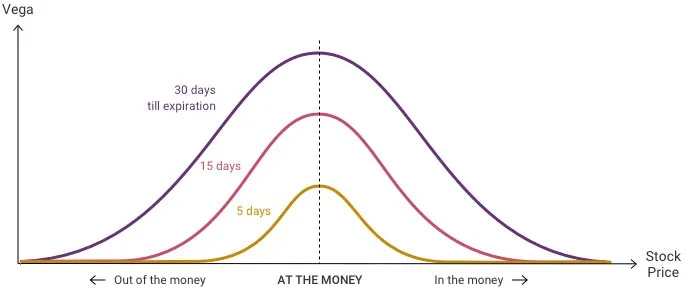
Analysis
- Options with a strike price closest to the underlying asset price (ATM) have the highest Vega value.
- The Vega of an option is related to the amount of Extrinsic Value (including Time Value and Implied Volatility) it has, “At the Money” options have the most Extrinsic Value and “OTM” options have the least Extrinsic Value.
Vega vs. Time to Expiration (Contract term)
Let’s look at this chart showing the impact of time on Vega’s growth.
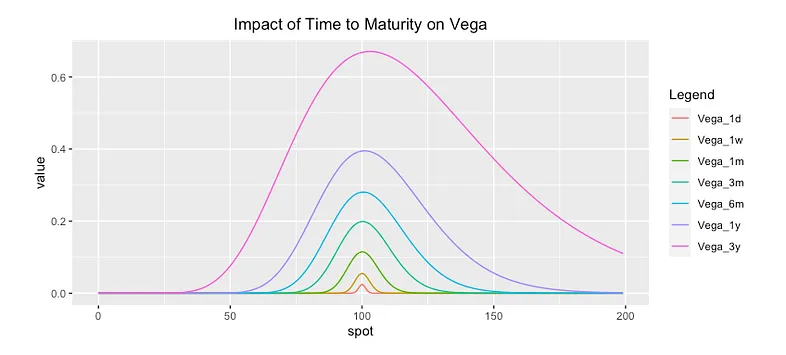
Analysis
Options with longer contract periods have greater Vega value. This means that long-term options will be more likely to be subject to price fluctuations that come from variations in the expected volatility index. The reason is because Options with longer expirations will have more Extrinsic Value.
To understand why options with higher Extrinsic Values have higher Vega values, let’s consider the following hypothetical situation:
|
Options |
Expected volatility |
Extrinsic Value |
Vega |
|---|---|---|---|
|
A |
first% |
$0.25 |
0.25 |
|
B |
first% |
$0.75 |
0.75 |
If the Extrinsic Value of both options were at $0, the expected volatility would be 0%. To reach Extrinsic Value = $0, option B must cost $0.75 while option A only costs $0.25 USD. Therefore, Option B has a larger Vega value.
Conclude
- Vega for all options is always positive because options increase in value as volatility increases and decrease in value as volatility decreases.
- When an option position exists in Vega, there will be both risk and potential. When you establish a short position or buy an option, your position affects the Vega of the entire market. And the total Vega position will depend on the sum of all the individual Vegas.
- Vega always has the same value for put options as for call options.
- The price of an option always increases with volatility.
- As Vega becomes smaller, volatility has less impact on option prices.
- The size of Vega itself depends largely on the relative value between the underlying asset price and the strike price as well as the option’s expiration time.
- Due to changes in expected volatility, the value of Vega may fluctuate even if the price of the underlying asset remains unchanged.
- Vega can increase with sudden changes in the price of the underlying asset.
- As the option gets closer to its expiration date, the value of Vega decreases.
- Vega is higher for options with more distant expiration dates. However, since longer-term options have higher premiums, Vega is actually higher for closer-term options if we look at the percentage gain or loss.
Glossary of Option terms
Underlying assets — Options contracts are predicting the price of this asset, such as Bitcoin.
Date due — The date the option will expire and be exercised, after this date, the contract is no longer valid.
Exercise price – The price at which the buyer has the right to buy or sell the underlying asset at maturity.
Option price (premium) — The price a buyer pays to a seller for the right to buy or sell an asset at the strike price on the expiration date.
In the money (ITM):
- For call options – this term is used when the strike price is less than the market value of the underlying asset.
- For put options – this term is used when the strike price is higher than the market value of the underlying asset.
At the money (ATM):
- For both call and put options – this term is used when the strike price is equal to the market value of the underlying asset.
Out of the money (OTM):
- For call options – this term is used when the strike price is higher than the market value of the underlying asset.
- For put options – this term is used when the strike price is lower than the market value of the underlying asset.
All options on Dopex are European style, which means they can only be exercised at expiration, unlike American style options can be exercised at any time until maturity.
About Dopex (Decentralized Option Exchange)
Dopex is a decentralized options trading protocol that aims to maximize liquidity, minimize losses for option writers, and maximize profits for passive options traders.
This article is done based on the combination of Dopex & Weakhand


