Dopex Essentials – Basic Options Theory (Part 6)

Welcome to the Dopex Essentials series that helps everyone get acquainted with the basics of options trading. Everyone should start with the first part of the series to grasp the knowledge throughout.

In this section, we will learn deeply about Option Gamma. There are quite a few problems related to calculations and some concepts are difficult to grasp This article will present the simplest way about Option Gamma.

Here is the complete list of parts of this Series:

In addition to this series, people can also refer to the following articles to better understand Option Trading and Dopex!

• Huge Growth Potential of Options in DeFi
• Exchange Between Weakhand & Dopex – Leading Options Platform on DeFi (Vietnamese)
• What is Dopex (DPX)? Overview of Dopex Cryptocurrency
• Series 9: Real Builder | Dopex – Growing Amid Difficult Insects

There is a glossary of terms at the end of the article, so if you come across unfamiliar terms, scroll down for reference!

What is gamma?

The gamma of an option measures the variability of the Delta value with changes in the price of the underlying asset. Gamma helps us answer this question – “For a given change in the price of the underlying asset, how will the Delta of the option change?”

Before going deeper into the article, we can relate some similarities between Delta and Gamma to the velocity and acceleration of a particle.

Remembering Velocity Theory

Velocity is the rate of change in distance (calculated as the change in distance divided by the time of movement). Analytically, velocity is the first derivative of the distance traveled.

Acceleration

Acceleration is the rate of change of velocity (i.e. change of velocity over time). Analytically, acceleration can be considered as the second derivative of the distance traveled or the first derivative of the velocity.

First order derivative

Similar to options, the change in the price of the option (or premium) based on the change in the price of the underlying asset is a quantifiable value called Delta. So Delta is the first derivative of the premium.

Second derivative

The variation in the value of Delta according to changes in the price of the underlying asset is a value called Gamma. Similar to the understanding of acceleration, Gamma is the second derivative of the premium, and is also the first derivative of Delta.

Surely readers may be concerned that calculating Delta and Gamma values ​​for options requires dealing with a lot of complex calculations (such as differential equations). Don’t worry because this article will not delve into that.

Funfact: Derivatives both means derivative financial instruments and also means “derivative”. The value of futures contracts and derivative options is calculated using “derivative” as a mathematical concept. Therefore futures and options contracts are called “Derivatives”.

Continue…

We have proven many times that the Delta of an option can continuously change in value in response to changes in the price of the underlying asset. Let’s look again at the Delta vs Spot Price chart mentioned in the previous article.

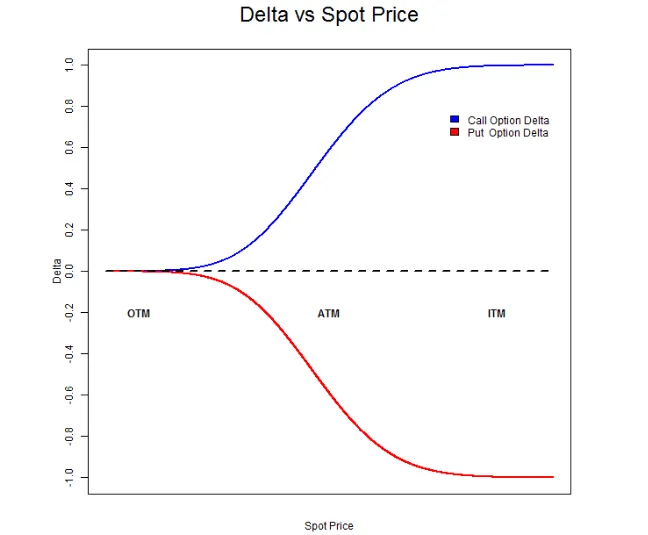
As can be seen from the chart above, Delta changes with the price of the underlying asset. The question is:

1. Why is the change in Delta value important?
2. How can we accurately estimate the change in Delta value?

We’ll tackle the second question first:

As mentioned above, Gamma is calculated as the derivative of the Premium in the option. Gamma is calculated by the change in Delta value per smallest change ($1) in the underlying asset price. Delta increases by an amount equal to the exact value of Gamma when the asset price increases by $1, and conversely, Delta decreases by an amount equal to the exact value of Gamma when the price of the underlying asset decreases by $1.

Coming to the first example:

Calculate

Obviously, when the price of HakhoToken moved from $8,326 to $8,396, the price of the option changed from $26 to $47 and the Delta of the option changed from 0.3 to 0.475.

With a change of 70 points, the moneyness of the option will move from Slightly OTM to ATM. Theoretically, that means the option’s Delta should change from 0.3 to a value closer to 0.5. That’s what happens in the example above.

Second example:

This time Let’s say HakhoToken increases another $70 from $8,396 to $8,466. What happens to our $8,400 call option (from now on called option Y)?

Third example:

Suppose HakhoToken falls by $50, what will happen to option Y? Let’s clarify each change:

Speed ​​(Gamma of Gamma)

You may wonder why the Gamma value remains constant in the above examples when in reality, the Gamma value also changes with the change in the price of the underlying asset.

The variation of the Gamma value due to changes in the price of the underlying asset is calculated by the third derivative of Premium, called “Speed” or “Gamma of Gamma” or “change in Gamma divided by change in price of the underlying asset”. However, we won’t go into that right now.

Moving on, as you may have noticed, unlike the Delta value, Gamma ALWAYS is positive, for both call and put options.

You may have heard traders use the term “Long Gamma”, which simply means that the trader is buying both call and put options. Or conversely, traders may use the term ‘Short Gamma’ when they sell both call and put options.

A few examples:

Question for you: The gamma of the ATM put option (called Option A) is 0.004. If the price of the underlying asset changes by $10, what do you think the new Delta will be?

Let us first recall that for ATM options, the magnitude of Delta is 0.5 and for put options, the Delta value is always negative. Therefore, the Delta value of option A is -0.5. We have determined that Gamma is always positive regardless of the option. The data from the questionnaire said The price of the underlying asset changes by $10, but it does not indicate the direction of the change, so let’s consider both scenarios (bullish and bearish).

Alpha case

Price of the underlying asset INCREASE $10

Alpha case

Price of the underlying asset REDUCE $10

Glossary of Option terms

Underlying assets — Options contracts are predicting the price of this asset, such as Bitcoin.

Date due — The date the option will expire and be exercised, after this date, the contract is no longer valid.

Exercise price – The price at which the buyer has the right to buy or sell the underlying asset at maturity.

Option price (premium) — The price a buyer pays to a seller for the right to buy or sell an asset at the strike price on the expiration date.

In the money (ITM):

• For call options – this term is used when the strike price is less than the market value of the underlying asset.
• For put options – this term is used when the strike price is higher than the market value of the underlying asset.

At the money (ATM):

• For both call and put options – this term is used when the strike price is equal to the market value of the underlying asset.

Out of the money (OTM):

• For call options – this term is used when the strike price is higher than the market value of the underlying asset.
• For put options – this term is used when the strike price is lower than the market value of the underlying asset.

All options on Dopex are European style, which means they can only be exercised at expiration, unlike American style options can be exercised at any time until maturity.

About Dopex (Decentralized Option Exchange)

Dopex is a decentralized options trading protocol that aims to maximize liquidity, minimize losses for option writers, and maximize profits for passive options traders.

This article is done based on the combination of Dopex & Weakhand