In this article, we will briefly discuss, as simply as possible, concepts such as the Black-Scholes Formula, Volatility Surfaces and Volatility Smiles. The article will focus on the meaning of these terms for options trading on Dopex.
Before continuing, be sure to read the first article in this series
because there are terms that you may not know but have been explained in the previous article. Here is the complete list of parts of this Series:
In addition, everyone can also refer to the following articles to better understand Option Trading and Dopex!
Black-Scholes model

Black-Scholes model
What is the Black-Scholes model?
Black-Scholes is a mathematical model built to theoretically value options contracts. Black-Scholes model use volatility of an option as input value to price that option.
Among them, the level The expected volatility of an option (often called Implied Volatility or Option Volatility) is understood as the expected future volatility of the option’s underlying asset price. The greater the expected volatility, the more likely the market is that the asset price is likely to increase or decrease.
Black-Scholes Assumption Set
Assumption set Black-Scholes are 6 conditions that must be satisfied for the Black-Scholes model to be meaningful. In the case of pricing an options contract with the underlying asset being a stock, those 6 conditions are:
- Holders of the shares in question must not be exempt from paying dividends
- The option to be exercised is a European-style option
- Financial markets are always efficient (Meaning that new information is quickly and fully reflected in the price of the asset, and therefore, trying to predict price movements to make a profit is difficult)
- All transactions are not authorized
- Interest rates remain unchanged
- Returns on the underlying stock are log-normally distributed
The Black Scholes model holds that The volatility of an option is constant. But in reality, it is always changing. Therefore, the premium price of options with the same exercise price and expiration time is often not the same as the theoretical price as calculated by the Black Scholes model.
In short, the volatility of an option is variable, and depends on two factors: (1) exercise price and (2) contract term. Therefore, it is possible to simulate the dependence of volatility on the above two variables into a three-dimensional chart called Volatility Surfaces.
Volatility Surfaces
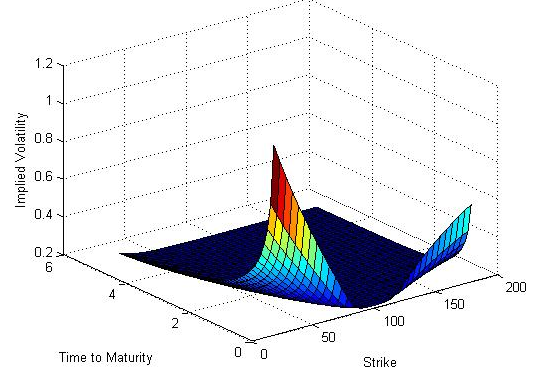
What are Volatility Surfaces?
Volatility Surfaces is a graph in three-dimensional space that shows expected volatility (Implied volatility) based on each value of the strike price (Strike) and contract term (Time to Maturity).
Assuming the Black-Scholes model is completely correct (Implied Volatility is constant), Volatility Surfaces must be a plane. However, in reality that is not the case, Volatility Surfaces are not flat and instead tend to change over time (because in real market conditions the six conditions of the Black Scholes model are not always satisfied).
The longer the contract term (or the time remaining until the contract’s expiration date), the lower the expected volatility. Options with shorter contract periods have significantly higher volatility.
For any given strike price, Implied volatility can increase or decrease over time until maturity, leading to a phenomenon known as Volatility Smiles.
Volatility Smiles
When the moneyness (correlation between the exercise price and the price of the underlying asset) is more OTM or ITM (and further away from ATM status), Implied volatility will increase.
What is Volatility Smiles?
Volatility Smiles is the shape of a histogram, showing the dependence of expected volatility on strike price. Specifically, the graph showing the value of expected volatility according to the exercise price is a U-shaped shape that resembles a smile, so this is called a volatility smile.
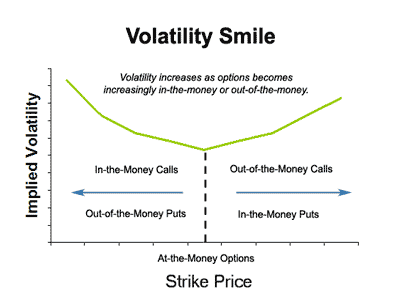
The Black-Scholes model does not predict Volatility Smiles. As mentioned earlier, Black-Scholes assumed that when plotted against different strike prices, Implied volatility would be a straight line parallel to the horizontal axis. In other words, for options with the same contract term and the same underlying asset, they all have the same expected volatility regardless of the exercise price.
However, the Black-Scholes Model is only theoretical. In reality, the market always has events that cause strong fluctuations. When these events take place, the price of the underlying asset changes and the potential for price volatility increases. While the price of the underlying asset directly affects the moneyness of the option. So the more ITM or OTM an option is, the higher the expected volatility is.
Dopex AMM pricing formula
The Dopex protocol has a number of flexible functions in providing liquidity, Inspired by successful AMM options platforms such as Deribit and Robinhood.
Dopex AMM uses assets from asset pools with Black-Scholes pricing, calculating volatility smiles to allow users to buy options based on strike price and future expiration.
The cost to buy options is also calculated on-chain based on the Black-Scholes model — using Implied volatility and asset prices provided by Chainlink — and passed through a function to calculate volatility smiles based on volatility actual assets and past data.
Problem at hand
The Implied volatility value is not objective if data from the order book is not available or if the options market for the underlying asset is inherently very illiquid. Currently, it is difficult to price options for illiquid assets in the options market such as BTC and ETH.
How Dopex solves it
Dopex’s pricing model is a decentralized consensus system, operated by many independent units, each providing different coefficients to calculate a single common volatility surface, with the condition that conditions that those units will not publicly disclose their coefficient calculation methods (to ensure objectivity).
Introducing Dopex
Dopex is a decentralized options protocol that aims to maximize liquidity, minimize losses for option writers, and maximize profits for passive option buyers.
This article is done based on the combination of Dopex & Weakhand


